洛谷P3382-三分法-题解

【模板】三分法

题目描述

如题，给出一个 $N$ 次函数，保证在范围 $[l, r]$ 内存在一点 $x$，使得 $[l, x]$ 上单调增，$[x, r]$ 上单调减。试求出 $x$ 的值。

输入格式

第一行一次包含一个正整数 $N$ 和两个实数 $l, r$，含义如题目描述所示。

第二行包含 $N + 1$ 个实数，从高到低依次表示该 $N$ 次函数各项的系数。

输出格式

输出为一行，包含一个实数，即为 $x$ 的值。若你的答案与标准答案的相对或绝对误差不超过 $10^{-5}$ 则算正确。

样例 #1

样例输入 #1

3 -0.9981 0.5
1 -3 -3 1

样例输出 #1

-0.41421

提示

对于 $100\%$ 的数据，$6 \le N \le 13$，函数系数均在 $[-100,100]$ 内且至多 $15$ 位小数，$|l|,|r|\leq 10$ 且至多 $15$ 位小数。$l\leq r$。

【样例解释】

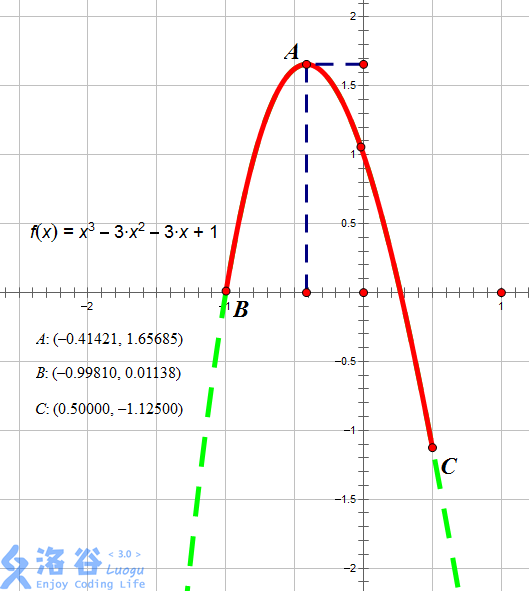
如图所示，红色段即为该函数 $f(x) = x^3 - 3 x^2 - 3x + 1$ 在区间 $[-0.9981, 0.5]$ 上的图像。

当 $x = -0.41421$ 时图像位于最高点，故此时函数在 $[l, x]$ 上单调增，$[x, r]$ 上单调减，故 $x = -0.41421$，输出 $-0.41421$。

P3382 【模板】三分法 - 洛谷

思路

这题作为一个模板题，肯定看一眼就知道用什么做了吧————没错，就是三分法！
对于这个表达式，我们取出他的中间值 mid ，以mid + 1e-6和mid - 1e-6为三分的边界，即将边界分为 $[l,mid - 10^{-6}),[mid - 10^{-6}, mid + 10^{-6}),[mid + 10^{-6}, r)$ 三个区间，然后每次舍去一次区间，再次三分，最后当 l 和 r 的精度偏差满足题意时，满足答案

C++代码

#include <algorithm>
#include <iostream>
#include <cmath>

using namespace std;

template<typename T>
T binary_search_answer(T l, T r,
                       const function<bool(const T &, const T &)> &isKeep,
                       const function<bool(const T &)> &check) {
    while (isKeep(l, r)) {
        T mid = (l + r) / 2;
        if (check(mid)) l = mid;
        else r = mid;
    }
    return l;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie();
    cout.tie();
    int n;
    double l, r;
    cin >> n >> l >> r;
    double arr[n+1];
    for (int i = 0; i <= n; i++) {
        cin >> arr[i];
    }
    auto f = [&](double x) {
        double res = 0;
        for(int i = 0; i <= n; i++)
            res += arr[i] * pow(x, n - i);
        return res;
    };
    cout << fixed << binary_search_answer<double>(l, r,
              [](const double &l, const double &r) 
              { return abs(r - l)  > 1e-6; },
              [&](const double &x) { return f(x+1e-6) > f(x-1e-6); });
    return 0;
}

AC截图

又或者，我们可以对函数进行求导，然后对其作用域进行二分法求其导函数的零点。对此，我们只需要修改上述代码的以下代码

修改前

auto f = [&](double x) {
    double res = 0;
    for(int i = 0; i <= n; i++)
        res += arr[i] * pow(x, n - i);
    return res;
};
cout << fixed << binary_search_answer<double>(l, r,
          [](const double &l, const double &r) 
          { return abs(r - l)  > 1e-6; },
          [&](const double &x) { return f(x+1e-6) > f(x-1e-6); });

修改后

auto f = [&](double x) {
    double res = 0;
    for(int i = 0; i <= n; i++)
        res += arr[i] * pow(x, n - i);
    return res;
};
auto fx = [&](double x) {
    //f'(x) = lim_{x->0} [f(x+dx)-f(x)]/dx
    return (f(x+1e-9) - f(x)) / 1e-9;
};
cout << fixed << binary_search_answer<double>(l, r,
          [](const double &l, const double &r) { return abs(r - l)  > 1e-6; },
          [&](const double &x) { return fx(x) > 0; });

AC截图就懒得贴了，这两种方法大差不差。C with STL的代码就不写了，相当就是把那两个匿名函数提出来，写成普通函数，然后把搜索的条件直接写到函数里面