洛谷P3958-奶酪-题解

【NOIP2017 提高组】 奶酪

题目背景

NOIP2017 提高组 D2T1

题目描述

现有一块大奶酪，它的高度为 $h$，它的长度和宽度我们可以认为是无限大的，奶酪中间有许多半径相同的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中，奶酪的下表面为 $z = 0$，奶酪的上表面为 $z = h$。

现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。

位于奶酪下表面的 Jerry 想知道，在不破坏奶酪的情况下，能否利用已有的空洞跑 到奶酪的上表面去?

空间内两点 $P_1(x_1,y_1,z_1)$、$P2(x_2,y_2,z_2)$ 的距离公式如下：

$\mathrm{dist}(P_1,P_2)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

输入格式

每个输入文件包含多组数据。

第一行，包含一个正整数 $T$，代表该输入文件中所含的数据组数。

接下来是 $T$ 组数据，每组数据的格式如下： 第一行包含三个正整数 $n,h,r$，两个数之间以一个空格分开，分别代表奶酪中空洞的数量，奶酪的高度和空洞的半径。

接下来的 $n$ 行，每行包含三个整数 $x,y,z$，两个数之间以一个空格分开，表示空洞球心坐标为 $(x,y,z)$。

输出格式

$T$ 行，分别对应 $T$ 组数据的答案，如果在第 $i$ 组数据中，Jerry 能从下表面跑到上表面，则输出 Yes，如果不能，则输出 No。

样例 #1

样例输入 #1

3 
2 4 1 
0 0 1 
0 0 3 
2 5 1 
0 0 1 
0 0 4 
2 5 2 
0 0 2 
2 0 4

样例输出 #1

Yes
No
Yes

提示

【输入输出样例 $1$ 说明】

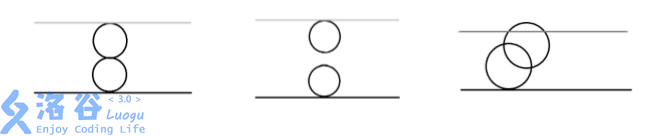
第一组数据,由奶酪的剖面图可见：

第一个空洞在 $(0,0,0)$ 与下表面相切；

第二个空洞在 $(0,0,4)$ 与上表面相切；

两个空洞在 $(0,0,2)$ 相切。

输出 Yes。

第二组数据,由奶酪的剖面图可见：

两个空洞既不相交也不相切。

输出 No。

第三组数据,由奶酪的剖面图可见：

两个空洞相交，且与上下表面相切或相交。

输出 Yes。

【数据规模与约定】

对于 $20\%$ 的数据，$n = 1$，$1 \le h$，$r \le 10^4$，坐标的绝对值不超过 $10^4$。

对于 $40\%$ 的数据，$1 \le n \le 8$，$1 \le h$，$r \le 10^4$，坐标的绝对值不超过 $10^4$。

对于 $80\%$ 的数据，$1 \le n \le 10^3$，$1 \le h , r \le 10^4$，坐标的绝对值不超过 $10^4$。

对于 $100\%$ 的数据，$1 \le n \le 1\times 10^3$，$1 \le h , r \le 10^9$，$T \le 20$，坐标的绝对值不超过 $10^9$。

P3958 [NOIP2017 提高组] 奶酪

思路

搜索

看到从一个点到另一个点，很容易就想到使用搜索算法了。这题数据量比较小，搜索时间复杂度也不会被卡，正向搜索和反向搜索都可以过。简单来说就是，枚举每个下表面上的点（或者上表面上的点），每次从这个点出发，搜索，如果能搜索到上表面的点（或者下表面上的点），则说明可以走通，有解。

C++代码

#include <iostream>
#include <vector>
#include <numeric>

using namespace std;
using i64 = long long;

struct pos {
    i64 x, y, z;
};
vector<bool> visited;
vector<pos> poss;
i64 t, n, h, r;

bool isNear(const pos &first, const pos &second) {
    return (first.x - second.x) * (first.x - second.x)
           + (first.y - second.y) * (first.y - second.y)
           + (first.z - second.z) * (first.z - second.z)
           <= 4 * r * r;
}
bool isYes = false;
void dfs(const i64 &begin) {
    if (isYes or visited[begin])
        return;
    visited[begin] = true;
    if (poss[begin].z + r >= h) {
        isYes = true;
        return;
    }
    for (int i = 1; i <= n; ++i)
        if (not visited[i] and isNear(poss[begin], poss[i]))
            dfs(i);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    cin >> t;
    while (t--) {
        cin >> n >> h >> r;
        isYes = false;
        vector<i64> starts;
        poss.resize(n + 1);
        visited.resize(n + 1);
        fill(visited.begin(), visited.end(), false);
        for (i64 i = 1; i <= n; ++i) {
            cin >> poss[i].x >> poss[i].y >> poss[i].z;
            if (poss[i].z <= r)
                starts.emplace_back(i);
        }
        for (auto &i: starts)
            dfs(i);
        cout << (isYes ? "Yes\n" : "No\n");
    }
    return 0;

}

并查集

除了搜索以外，我们也可以用并查集来进行查找，预先将$n+1$和$n+2$设为底面和顶面，然后先将底面和顶面的节点合并到$n+1$和$n+2$所在的集合里，紧接着遍历每个点和其他点，如果相邻就合并。最后判断$n+1$和$n+2$是否在一个集合里即可

C++代码

#include <iostream>
#include <vector>
#include <numeric>

using namespace std;

template<typename T>
class UnionFindSet {
    vector<T> trees, size;
public:
    explicit UnionFindSet(const T &len = 0) : trees(len * 2), size(len * 2, 1) {
        iota(trees.begin(), trees.begin() + len, len);
        iota(trees.begin() + len, trees.end(), len);
    }

    int find(const T &x) {
        T tmp;
        for (tmp = x; trees[tmp] != tmp; tmp = trees[tmp]);
        return tmp;
    }

    void unite(const T &x, const T &y) {
        T &&fx = find(x), &&fy = find(y);
        size[fx] <= size[fy] ? trees[fx] = fy : trees[fy] = fx;
        if (size[fx] == size[fy] and fx != fy)
            size[fy]++;
    }

    void earse(const T &x) {
        --size[find(x)];
        trees[x] = x;
    }

    void move(const T &x, const T &y) {
        T &&fx = find(x), &&fy = find(y);
        if (fx == fy) return;
        trees[x] = fy;
        --size[fx], ++size[fy];
    }
};

using i64 = long long;

struct pos {
    i64 x, y, z;
};

bool isNear(const pos &first, const pos &second, const i64 &r) {
    return (first.x - second.x) * (first.x - second.x)
           + (first.y - second.y) * (first.y - second.y)
           + (first.z - second.z) * (first.z - second.z)
           <= 4 * r * r;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    i64 t, n, h, r;
    cin >> t;
    while (t--) {
        cin >> n >> h >> r;
        UnionFindSet<i64> ufs(n + 3);
        vector<i64> xs(n + 1), ys(n + 1), zs(n + 1);
        for (i64 i = 1; i <= n; ++i) {
            cin >> xs[i] >> ys[i] >> zs[i];
            if (zs[i] <= r)
                ufs.unite(i, n + 1);
            if (zs[i] + r >= h)
                ufs.unite(i, n + 2);
        }
        for (i64 i = 1; i <= n; ++i)
            for (i64 j = i + 1; j <= n; ++j)
                if (isNear({xs[i], ys[i], zs[i]}, {xs[j], ys[j], zs[j]}, r))
                    ufs.unite(i, j);
        cout << (ufs.find(n + 1) ^ ufs.find(n + 2) ? "No\n" : "Yes\n");
    }
    return 0;
}